Reducing the bias from on the inverse probability of treatment weighting (IPTW)
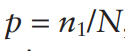
When using observational data, assignment to a treatment group is non-random and causal inference may be difficult. One common approach to addressing this is propensity score weighting where the propensity score is the probability that a person is assigned to the treatment arm given their observable characteristics. This propensity is often estimated using a logistic regression of individual characteristics on a binary variable of whether the individual received the treatment or not. Propensity scores are often used that to by applying inverse probability of treatment weighting (IPTW) estimators to obtain treatment effects adjusting for known confounders.
A paper by Xu et al. (2010) shows that using the IPTW approach may lead to an overestimate of the pseudo-sample size and increase the likelihood of a type I error (i.e., rejecting the null hypothesis when it is actually true). The authors claim that robust variance estimators can address this problem but only work well with large sample sizes. Instead, Xu and co-authors proposed using standardized weights in the IPTW as a simple and easy to implement strategy. Here is how this works.
The IPTW approach simply examines the difference between the treated and untreated group after applying the IPTW weighting. Let the frequency that someone is treated be:
where n1 is the number of people treated and N is the total sample size. Let z=1 if the person is treated in the data and z=0 if the person is not treated. Assume that each person has a vector of patient characteristics, X, that impact the likelihood of receiving treatment. Then one calculate the probability of treatment as:
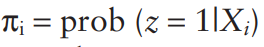
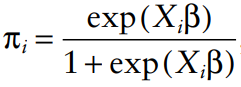
Under standard IPTW, the weights used would be:

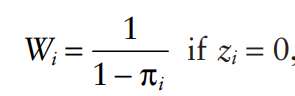
Xu and co-authors create a simulation to show that the type 1 error is too high–often 15% to 40%. To correct this, one could use standardized weights (SW) as follows:


The former is used for the treated population (i.e., z=1) and the latter is used in the untreated population (z=0). The authors show that under the standardized weights, the rate of type 1 errors is approximately 5% as intended. In fact, the authors also show that standardized weighting often outperforms robust variance estimators as well for estimating main effects.
For more information, you can read the full article here.





